LESGO
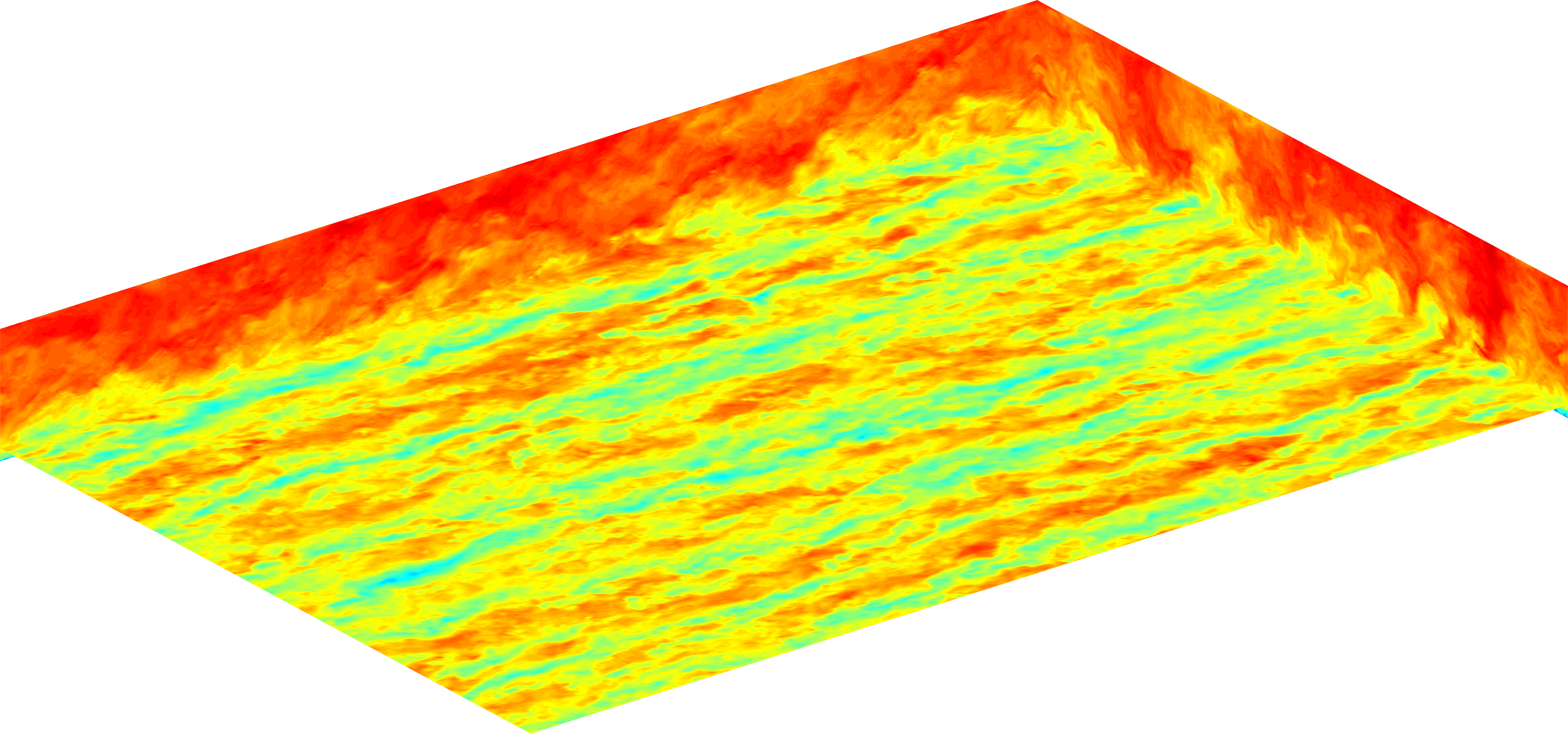
LESGO is a parallel pseudo-spectral large-eddy simulation code.
Subgrid scale models
The subgrid scales are modeled using an eddy viscosity model for the deviatoric part of the subgrid stress tensor
\[\tau_{ij} = - 2 \nu_T \tilde{S}_{ij}, \]
where \( \tilde S_{ij} = \frac{1}{2} \left( \partial_j \tilde u_i + \partial_i \tilde u_j \right) \) is the resolved strain rate tensor. The eddy viscosity is usually given using the Smagorinsky relationship \( \nu_T = (C_{s,\Delta} \Delta)^2 | \tilde{S} | \), where the strain rate magintude is \( | \tilde{S} | = \sqrt{ 2\tilde S_{ij} \tilde S_{ij} }\).
LESGO includes five subgrid models to determine the coefficient \( C_{s,\Delta} \):
-
The Smagorinsky model with the Mason wall damping model specifies \( C_{s,\Delta} \) using \[ \lambda^{-n} = \lambda_0^{-n} + \left[ \kappa \left( z + z_0 \right) \right]^{-n} \] where \( \lambda = C_{s,\Delta} \Delta \) is the subgrid scale mixing length, \( \lambda_0 = C_{0} \Delta \) is the mixing length in the freestream, \( \kappa \) is the von Kármán constant and \(z_0\) is the surface roughness height. The default values are \(C_0 = 0.16\), which corresponds to the Lilly-Smagorinsky for isotropic homogeneous turbulence, and \(n = 2\).
-
The dynamic model dynamically changes the Smagorinsky coefficient \( C_{s,\Delta}(z,t) \) by test filtering the flow field at a larger scale, assuming scale invariance, and averaging over horizontal planes.
-
The scale-dependent model dynamically changes the Smagorinsky coefficient \( C_{s,\Delta}(z,t) \) by test filtering the flow field at two larger scales and averaging over horizontal planes. Unlike the dynamic model, the scale-dependent model does not assume scale invariance.
-
The Lagrangian scale-similarity model dynamically changes the Smagorinsky coefficient \( C_{s,\Delta}(\mathbf{x},t) \) by test filtering the flow field at a larger scale, assuming scale invariance, and averaging over Lagrangian trajectories.
-
The Lagrangian scale-dependent model dynamically changes the Smagorinsky coefficient \( C_{s,\Delta}(\mathbf{x},t) \) by test filtering the flow field at two larger scales and averaging over Lagrangian trajectories. Unlike the Lagrangian scale-similarity model, the Lagrangian scale-dependent model does not assume scale invariance.
References
Bou-Zeid E, Meneveau C, Parlange MB. “A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows.” Physics of Fluids 17 (2005). 025105.
Porté-Agel F, Meneveau C, Parlange MB. “A scale-dependent dynamic model for large eddy simulation: applications to a neutral atmospheric boundary layer.” Journal of Fluid Mechanics 415 (2000). 261-284.
Meneveau C, Lund T, Cabot W. “A Lagrangian dynamic subgrid-scale model of turbulence.” Journal of Fluid Mechanics 319 (1996). 353.
Germano M, Piomelli U, Moin P, Cabot WH. “A dynamic subgrid‐scale eddy viscosity model.” Physics of Fluids A: Fluid Dynamics 3 (1991). 1760-1765.
Mason PJ, Thomson DJ. “Stochastic backscatter in large-eddy simulations of boundary layers.” Journal of Fluid Mechanics 242 (1992). 51.
Smagorinsky J. “General circulation experiments with the primitive equations: I. The basic experiment.” Monthly Weather Review 91 (1963). 99-164.